
The correct terminology is shown in the slide below If the left hand side (LHS) equals the right hand side (RHS) then the identity is proved to be true.
#Og base 3 of x in graphmatica how to
(That would be 315 degrees, but I don't know how to get a degrees sign on here either.)īy using the identity cos( a - b) = cos acos b + sin asin b ,Ĭos(360 - 45) = cos360cos45 + sin360sin45īy using the identity cos( a + b) = cos acos b - sin asin b ,Ĭos(270 + 45) = cos270cos45 - sin270sin45 By the way, I'm sure there's a way to use greek letters, but I couldn't find it so I'm substituting a for alpha and b for beta.īy using the identity sin( a - b) = sin acos b - cos bsin a,ĭetermine the exact value of cos(315). Well, I basically just copied what the examples were in the green Mickelson book, but changed the numbers, but just working through the examples and my own really helped me understand them better. Remember!!! Always keep the stick on the ice. Any questions or comments on how I can improve PLEASE let me know.
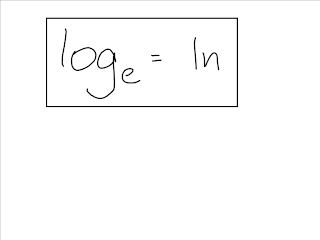
Always note the signs you apply to the final answer so you make sure you have it in the right quadrant.īelow is just another example of solving double angles using exact values. So Max simply input the values for theta into another formula from our exam formula sheet, and solved for cosine and sine. In this picture below, they wanted to know the value of 2(theta). Knowing these triangles will come in very handy. Also take not of a 30, 60, 90 triangle with lengths of 3, 4, and a hypotenuse of 5. I found this part very helpful and makes learning identities easier to understand!Īnother things that I found useful in today's lesson is to always keep in mind the key triangles that we learned at the start of the year. Max took all the equations given to us in our exam formula sheet and showed how they derived the formula. Today we did some more work with double angle identities. Maksymchuk continued on his journey to explain identities. I never had time yesterday and today it took me awhile to upload images due to the sweet sun computers.Īnywho, today Mr. Hope these notes were helpful and have a great day! On the fouth and fifth slides he graphed examples of logarithmic functions, and on the following slide he gave us a list of 8 common log properties.Įxercise 20 #'s 1-12 and Exercise 21 #'s 1-8 are due for tomorrow! This is because if you try to sub in a +2 for the x value you wont arrive at a -4 and if you sub in a -2 for x, you will end up with a +1/2

In the third screen shot he showed us a logarithmic function that does not exist.

In the second screen shot, he then went on to show us how to write exponential funtions in logarithmic notation and vice versa. X = b^y -> x is the argument, b is the base, and y is the argument. He also explained what the parts of a logarithmic function were. He began with explaining to us what a log was, and it is really just another type of notation that can be used to express things such as really big numbers and it is the inverse of an exponential function. Everything on the website is FREE.So as you all know, today Mr. I have many other topics from Basic, Intermediate, and College Algebra that are explained in detail, with many of these topics explained on video as well.
#Og base 3 of x in graphmatica free
If you don't have RealPlayer, then it is a FREE download. All of this is FREE if you have RealPlayer. In addition to my written explanations of this topic, there is a video explanation from my own classes from before I retired.

Besides this, many of my exercises are solved IN COLOR in the MATH IN LIVING COLOR pages that go with this. I have a complete explanation of Logarithms that I think you will find my explanation a lot easier to understand than traditional textbooks. On my Homepage, look for the link "Basic, Intermediate, and College Algebra: One Step at a Time." Then choose "College Algebra", then "Chapter 4 (Logarithms)", and see Section 4.04. However, you cannot have the log of a negative number, so x=-9 is rejected.įor additional help with LOGARITHMS, please see my own website by clicking on my tutor name "rapaljer" anywhere in. There appear to be two answers: x=-9 and x=3. You can put this solution on YOUR website!įirst, use the Law of Logarithms to combine the logs:


 0 kommentar(er)
0 kommentar(er)
